线段光栅化的'diamond-exit' rule

“diamond-exit” rule（菱形退出法则）是 OpenGL 在理想状态下线段光栅化的标准。

定义

经典的Bresenham 算法非常高效，但真实渲染过程中，一个线段的起点和终点往往都不在整数坐标轴上。

对于一个像素而言，菱形区域可以如下定义：

\[R_f = \lbrace (x, y) | |x - x_f| + |y - y_f| < 1/2 \rbrace\]

其中 \(x_f\) 和 \(y_f\) 是坐标轴上的点。

在手册中有这么一张图可以形象地说明菱形区域。

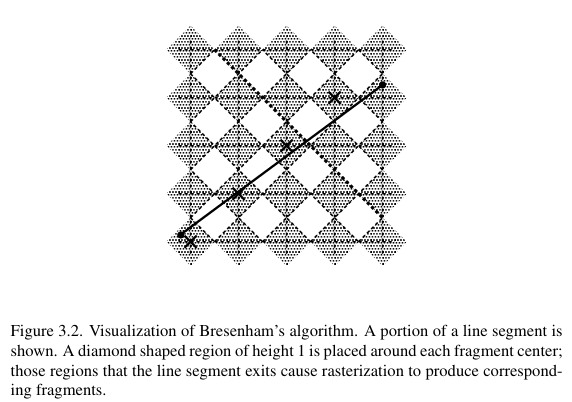
顾名思义，一条从起点到终点的线段，当其从这个菱形“退出”时，代表这个菱形的像素应该被渲染。当起止点都在坐标上时，”diamond-exit” rule 与 Bresenham 算法的区别在于最后一个像素不会被绘制，且当绘制首尾相接的线段时，不会重复绘制同一个点。

当端点位于菱形边界上时，通过一个小量扰动解决：

\[(x_a, y_a) \to (x_a, y_a) - (\epsilon, \epsilon^2)\]

局限

实际上 “diamond-exit” rule 是很难实现的，尤其对于边界而言。在实际使用的算法中，允许一定的误差：

1. 计算出的片段（fragment，也可以说是像素）的x和y坐标与法则的结果不超过1个单位的偏离；
2. 计算出的片段总数与法则的结果不超过1个单位的差异；
3. 对 x-major 的线段，不会在同一横坐标绘制2个片段（y-major 同理）；
4. 如果两个线段共享一个端点，并且如果两个线段都是 x-major 或都是 y-major，此时不允许产生重复的片段，也不允许省略片段，以避免破坏两个相连线段的连续性。

只要满足以上规则，我们可以认为这个光栅化的实现是符合 GL 的标准的。