平面反射(Planar Reflection)
平面反射(Planar Reflection)用于模拟光线在一个平面表面(如水面、镜子或任何光滑表面)上的反射效果。这种技术通常用于生成真实感的反射效果,广泛应用于视频游戏、虚拟现实以及视觉特效中
空间变换思路
有一个比较直观的方法是,将需要渲染的顶点全部变换相对于平面做一个镜面对称,相当于为model矩阵增加一个对称的步骤,然后再进行后续的变换。
绝大多数引擎默认都是这样实现的,反射变换可以用一个矩阵表示,将反射变换矩阵传入顶点着色器中,然后增加一次矩阵运算即可。
反射变换矩阵推导
这里给出反射变换矩阵的一种简单推导:
- 反射面\(S\),其法线\(\vec{n} = (x_n, y_n, z_n)\),\(\|\vec{n}\| = 1\)
- 空间内一点 \(P = (x, y, z)\) 关于反射面 \(S\) 的对称点为 \(P' = (x', y', z')\)
- 原点\(O\)到平面\(S\)的距离记为\(d\),有平面方程\(\vec{OA} \cdot \vec{n} - d = 0\),\(A\)为平面上任意一点
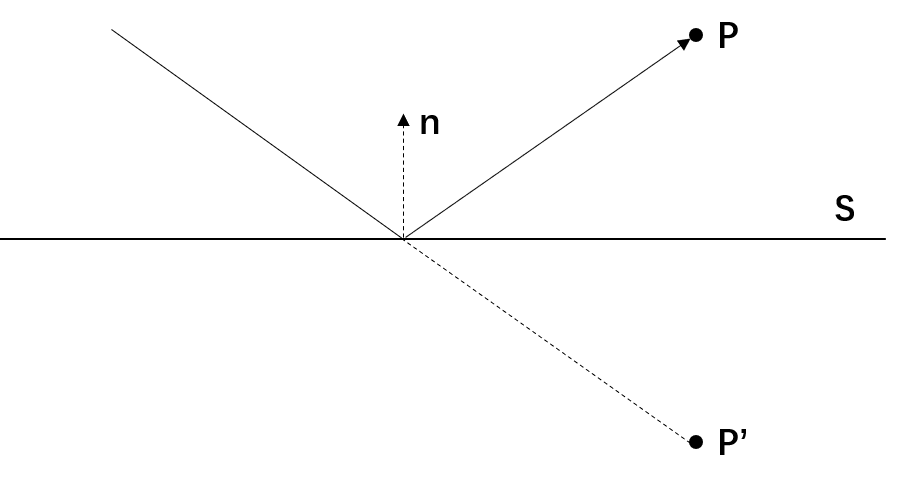
对称有2个约束条件:
- \[\vec{P'P} \parallel \vec{n}\]
- 点 \(P\) 和 \(P'\) 的中点在平面内
条件1可以表示为:
\[\frac{x - x'}{x_n} = \frac{y - y'}{y_n} = \frac{z - z'}{z_n} = \frac{\vec{P'P} \cdot \vec{n}}{\|\vec{n}\|}\]根据条件2,结合点\(P\)到平面的距离:
\[\frac{\vec{P'P} \cdot \vec{n}}{\|\vec{n}\|} = 2 \frac{\vec{OP} \cdot \vec{n} - d}{\|\vec{n}\|} = 2 (xx_n + yy_n + zz_n - d)\]综合2个条件,有:
\[\frac{x - x'}{x_n} = \frac{y - y'}{y_n} = \frac{z - z'}{z_n} = 2 (xx_n + yy_n + zz_n - d)\]显然\(x', y', z'\)都可用已知的\(x, y, z\)和\(x_n, y_n, z_n, d\)表示,整理可得:
\(x' = (1 - 2x_n^2)x - (2x_ny_n)y - (2x_nz_n)z + 2x_nd\) \(y' = - (2x_ny_n)x + (1 - 2y_n^2)y - (2y_nz_n)z + 2y_nd\) \(z' = - (2x_nz_n)x - (2y_nz_n)y + (1 - 2z_n^2)z + 2z_nd\)
其中\(d\)的正负与法线方向有关。
综上,反射变换矩阵:
\[\begin{bmatrix} x' \\ y' \\ z' \\ 1 \end{bmatrix} = \begin{bmatrix} 1 - 2x_n^2 & -2x_ny_n & -2x_nz_n & 2x_nd \\ -2x_ny_n & 1 - 2y_n^2 & -2y_nz_n & 2y_nd \\ -2x_nz_n & -2y_nz_n & 1 - 2z_n^2 & 2z_nd \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix}\]视角变换思路
有很多游戏并不是对物体进行反射变换,而是通过重置相机的view和projection矩阵来实现反射效果。
这种方法只需要修改传入的view和projection矩阵,就可以得到反射效果的render texture。
反射相机
得到反射相机可以通过以下步骤:
- 将相机变换至平面的局部坐标系;
- 将相机的y轴翻转,位置和方向都要翻转,得到反射相机的view矩阵;
- projection矩阵不变;
事实上反射相机不需要一个真的相机,比如在unity中复制一个相机、然后修改参数这种方法是不必要的,只需要计算view和projection矩阵,然后用类似于commands.SetViewProjectionMatrices(view, proj)这样的方法传入即可。
斜截视锥体
再前面的两个思路中会忽略一个问题,在得到反射的render texture时,会将整个视锥体的内容,包括本来应该被平面遮挡的几何体都渲染到render texture中。在正常的几何体渲染中,由于存在深度测试,不会存在问题;但是在反射的render texture中,不应该包含被遮挡的几何体。
通常的解决办法是,在计算投影矩阵时,将反射面设置为近截面(同时影响远截面),从而剔除掉被遮挡的几何体。
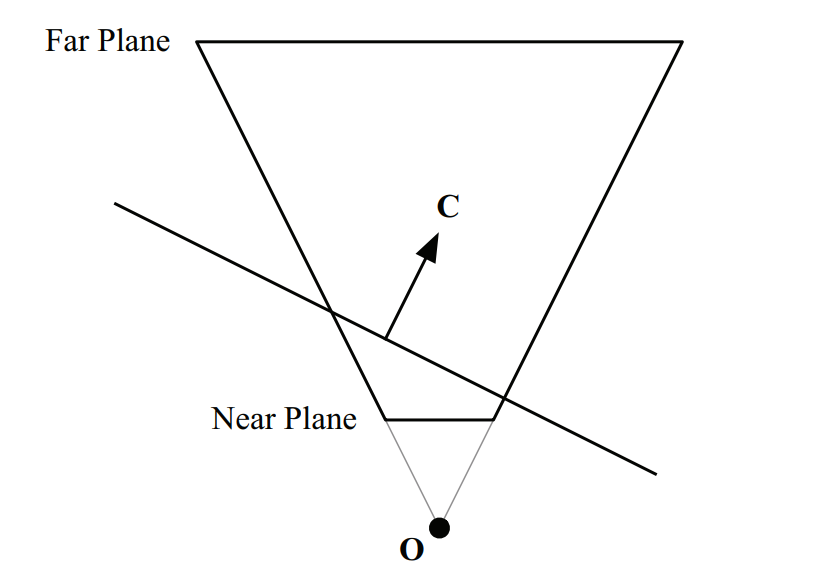
斜截视锥体的投影矩阵
原论文:Oblique View Frustum Depth Projection and Clipping
近平面替换
投影矩阵\(M\)将顶点从camera space变换到clip space,顶点在clip space中的\(x,y,z,w\)值分别由\(M\)的每一行决定。用\(M_i\)表示\(M\)的第\(i\)行:
\[M = \begin{bmatrix} M_1 \\ M_2 \\ M_3 \\ M_4 \end{bmatrix}\]平面可以表示为\(C = (N_x, N_y, N_z, -\mathbf{N} \cdot Q)\),其中\(\mathbf{N}=(N_x, N_y, N_z)\)是单位法线,\(Q\)是平面上任意一点。平面向量并非是像普通点那样的逆变(contravariant)向量,而是协变(covariant)向量,因此将平面从一个坐标系变换至另一个坐标系时,需要用逆转置变换:
\[C' = (M^{-1})^T C\]由此可以得到:
\[C = ((M^{-1})^T)^{-1} C' = M^T C'\]而clip space中的平面向量\(C'\)很容易得到,比如\(C' = (0, 0, 1, 1)\)表示近平面。对于任意平面\(C' = (c_1, c_2, c_3, c_4)\),可以得到:
\[C = \begin{bmatrix} M_1^T M_2^T M_3^T M_4^T \end{bmatrix} \begin{bmatrix} c_1 \\ c_2 \\ c_3 \\ c_4 \end{bmatrix} = c_1 M_1 + c_2 M_2 + c_3 M_3 + c_4 M_4\]对于视锥截面,有如下表格:
| Frustum Plane | Clip-space Coordinates | Camera-space Equation |
|---|---|---|
| Near | (0, 0, 1, 1) | M4 + M3 |
| Far | (0, 0, -1, 1) | M4 - M3 |
| Left | (1, 0, 0, 1) | M4 + M1 |
| Right | (-1, 0, 0, 1) | M4 - M1 |
| Bottom | (0, 1, 0, 1) | M4 + M2 |
| Top | (0, -1, 0, 1) | M4 - M2 |
如果要将近平面替换为任意平面\(C\),需要满足\(C = M_4 + M_3\),由于\(M_4\)会影响后续透视除法,因此只能调整\(M_3\):
\[M_3' = C - M_4\]远平面调整
按照上面的思路,可以得到:
\[F = M_4 - M_3' = 2 M_4 - C\]如图所示,显然不合理:
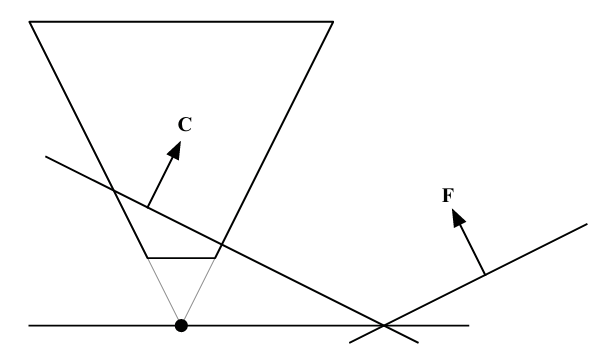
这种情况下近平面和远平面不再平行,但这是不可避免的,但是这种视锥是非常反直觉的。既然对平面向量乘一个缩放系数不会改变平面,那我们可以将近平面的向量乘\(a\),使得改变后的视锥能够包含原视锥,同时使远近平面之间的夹角尽可能小,如图所示。
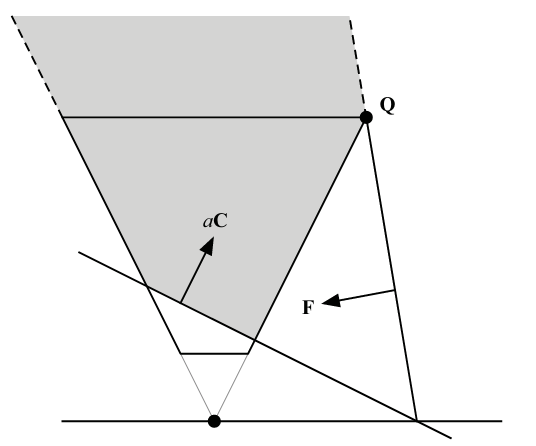
令\(C' = (M_{-1})^T C\)为新的进平面在clip space中的向量,图中视锥的拐角在clip space中的坐标为:
\[Q' = (sgn(C_x'), sgn(C_y'), 1, 1)\]然后将\(Q'\)变换回camera space:
\[Q = M^{-1} Q'\]让\(Q\)在远平面上,即\(F\cdot Q = 0\),可以得到:
\[a = \frac{2M_4 \cdot Q}{C \cdot Q}\]综上:
\[F = 2 M_4 - aC\] \[M_3' = aC - M_4\]修改投影矩阵
标准的透视投影矩阵为:
\[M = \begin{bmatrix} \frac{2n}{r-l} & 0 & \frac{r+l}{r-l} & 0 \\ 0 & \frac{2n}{t-b} & \frac{t+b}{t-b} & 0 \\ 0 & 0 & \frac{-(f+n)}{f-n} & \frac{-2fn}{f-n} \\ 0 & 0 & -1 & 0 \end{bmatrix}\]其逆矩阵为:
\[M^{-1} = \begin{bmatrix} \frac{r-l}{2n} & 0 & 0 & \frac{r+l}{2n} \\ 0 & \frac{t-b}{2n} & 0 & \frac{t+b}{2n} \\ 0 & 0 & 0 & -1 \\ 0 & 0 & \frac{f-n}{2fn} & \frac{f+n}{2fn} \end{bmatrix}\]可得:
\[M_3' = aC - M_4 = \frac{2M_4\cdot Q}{C\cdot Q} C - M_4\] \[Q = M^{-1}Q' = \begin{bmatrix} sgn(C_x)\frac{r-l}{2n}+\frac{r+l}{2n} \\ sgn(C_y)\frac{t-b}{2n}+\frac{t+b}{2n} \\ -1 \\ \frac{1}{f} \end{bmatrix}\]一般情况
一般来说,反射平面会垂直于\(z\)轴,即\(C = (0, 0, -1, -d)\),此时有:
\[M_3' = (0,0,-\frac{f+d}{f-d},-\frac{2fd}{f-d})\]深度变化
在原文中还讨论了深度变化的问题,结论是在实际情况下斜截视锥体对深度测试影响不大,这里不再详细讨论。