Jiajun's Blog

FSR (FidelityFX Super Resolution)

•
  • Computer-Graphics

FSR是AMD提出的超分辨率技术，是一种非ML的超分辨率方法，能够在各种硬件上运行。

FSR

FSR（FidelityFX Super Resolution）分为两个pass，EASU和RCAS。

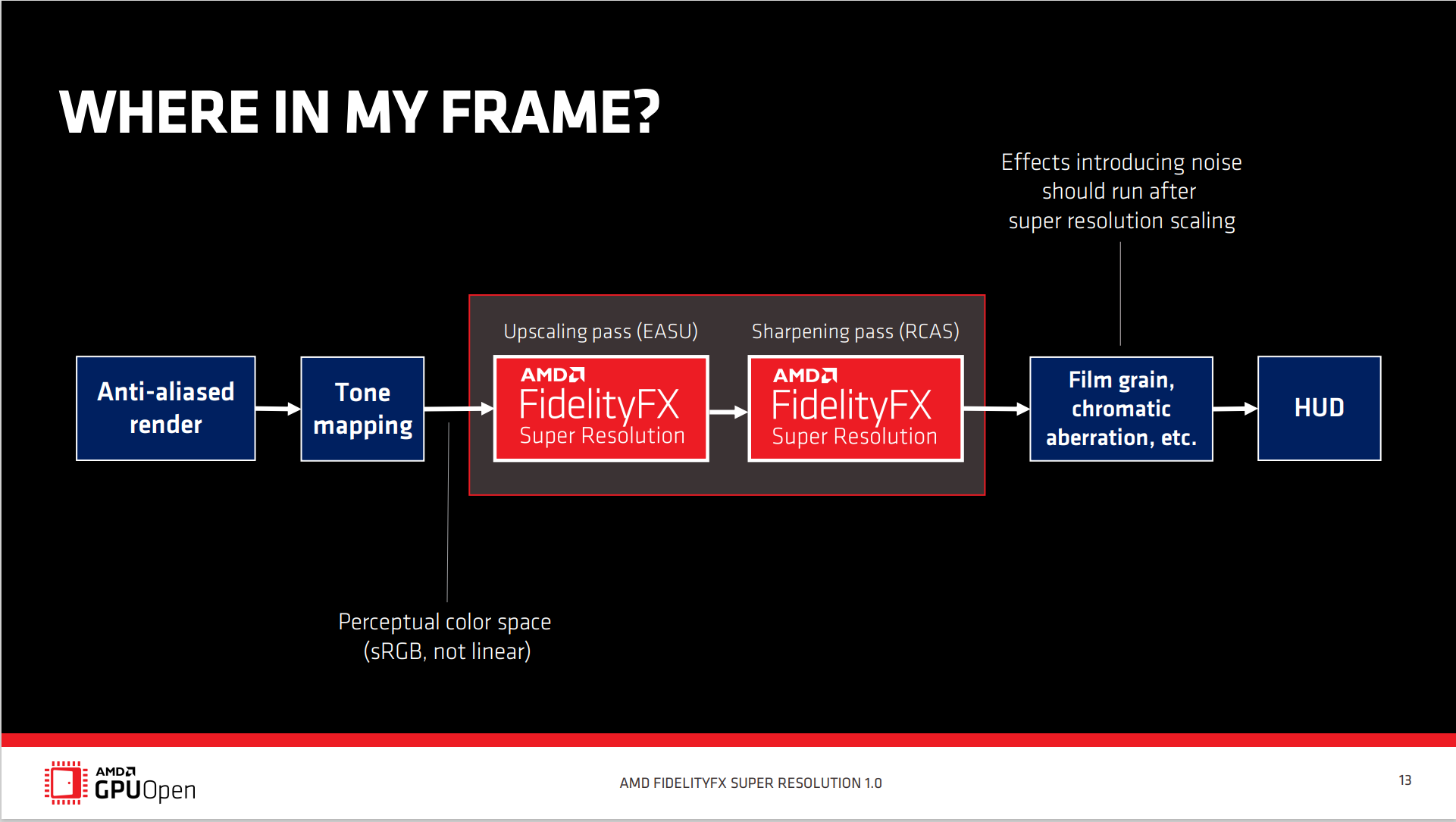
EASU (Edge Adaptive Spatial Upsampling)

EASU为一个上采样操作。上采样的过程中，像素\(P\)的公式为：

\[f(P) = \frac{\sum_i{f(Q_i)H(Q_i)}}{\sum_i{H(Q_i)}}\]

\(Q\)为\(P\)在原图对应的像素，\(Q_i\)为其邻域像素。

\(H(Q_i)\)为权重函数，需要根据是否为边缘像素来计算。这个函数需要满足，对一个像素而言：

  1. 非边缘时，权重为正数；
  2. 边缘时，边缘像素的权重需要为负数。

类似于一个高频滤波器。

权重函数

EASU使用Lanczos插值核作为权重函数。Lanczos插值核的公式为：

\[L(x) = \frac{sin(\pi x)sin(\pi x/a)}{(\pi x)^2}, |x| < a\]

EASU使用Lanczos2，即\(a=2\)时：

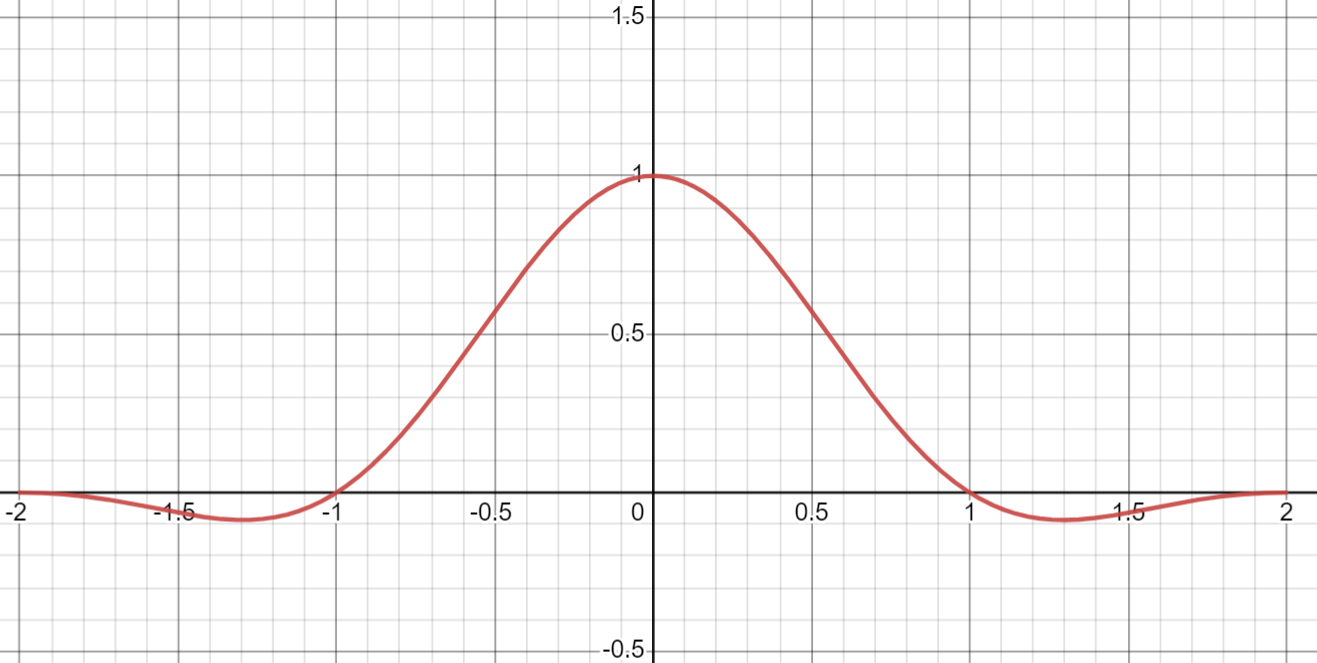
在\(x=1\)处展开，并添加一个系数\(\omega\)：

\[L(x) = \left[\frac{25}{16}\left(\frac{2}{5}x^2 - 1\right)^2 - \left(\frac{25}{16} - 1\right)\right] (\omega x^2 - 1)^2\]

该权重函数在\(\omega\)越小时，在\([1,2]\)区间的极值越小：因此该像素越接近边缘，\(\omega\)越小。

从边缘确定权重

从图像中可以看到，在正半轴，权重函数有\(1, 1/\sqrt{\omega}, 2\)三个极值点。EASU的权重计算只使用\(x\in[1,1/\sqrt{\omega}]\)的区间。

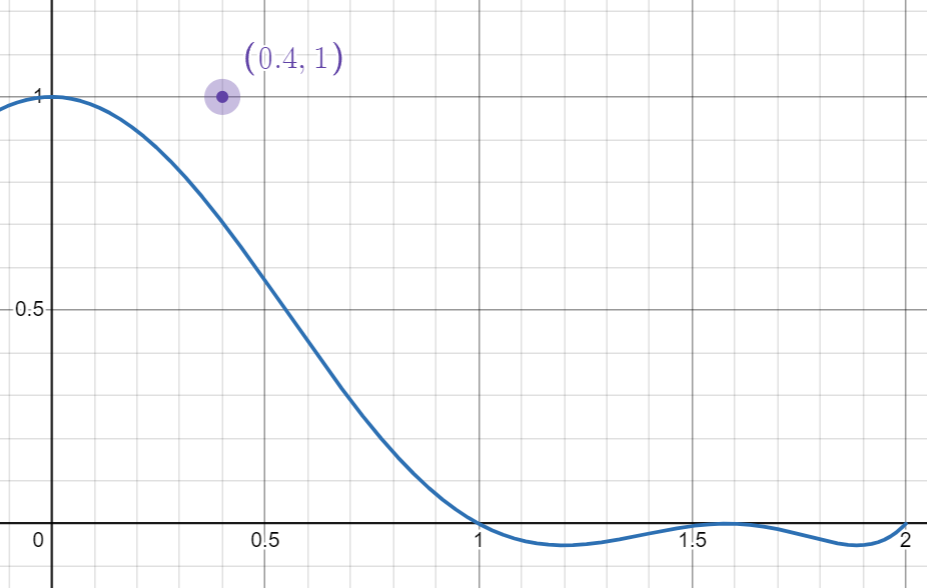
通过计算像素与周围像素的差分，然后归一化到\([0,1]\)区间，得到边缘特征\(len\)，越边缘的像素，\(len\)越大。EASU给出了一个\(len\)与\(\omega\)的线性关系：

\[\omega = \frac{1}{2} + \left(\left(\frac{1}{4} - 0.04\right) - 0.5\right)len\]

这个关系是一个经验公式，最终\(\omega\)会处于\((0.25, 0.5]\)区间。不用更大的\(\omega\)是为了防止\(x\in[1,1/\sqrt{\omega}]\)的区间过小。

双线性插值

能够直接计算差分是一种比较理想的情况，但是上采样在原图的采样点往往不是整数，因此EASU采用了一种双线性插值的策略计算\(len\)。

图中\(O=floor(Q)\)，分别以下面f、j、k、g为中心计算差分，然后双线性插值得到\(len\)。

\[len = (1-u)(1-v)f_1 + u(1-v)f_2 + uv f_3 + (1-u)v f_4\]

旋转采样

为了适应边缘的角度，EASU还进行了旋转。首先计算\(xy\)的梯度：

\[D_x = f(Q_{x-1,y}) - f(Q_{x+1,y})\] \[D_y = f(Q_{x,y-1}) - f(Q_{x,y+1})\]

梯度可以在之前计算差分的时候一起求出来，而且也经过了双线性插值。

然后将采样核按梯度方向旋转：

\[x = x \cos(\theta) + y \sin(\theta)\] \[y = -x \sin(\theta) + y \cos(\theta)\]

这里源码中有一个特判，方向向量的模很小时直接返回。

旋转后EASU给了一个很魔法的缩放：

\[Stretch = \frac{1}{\max(\|\sin(\theta)\|, \|\cos(\theta)\|)}\] \[S_x = 1 + (Stretch - 1) * len\] \[S_y = 1 - 0.5 * len\]

将每一个\(Q_i\)到\(Q\)的欧氏距离和\(\omega\)带入权重的计算公式，求加权平均即可得到\(P\)的颜色值。

\[L(x) = \left[\frac{25}{16}\left(\frac{2}{5}x^2 - 1\right)^2 - \left(\frac{25}{16} - 1\right)\right] (\omega x^2 - 1)^2\] \[f(P) = \frac{\sum_i{f(Q_i)H(Q_i)}}{\sum_i{H(Q_i)}}\]

最后，对求出的颜色做一个限制，减少ringing artifacts。EASU的做法是将颜色的最大最小值限制在最接近的2x2个格子的最大最小值之间。

RCAS (Robust Contrast Adaptive Sharpening)

RCAS是一个简单的锐化操作。锐化核为：

+---F---+---+
|   | w |   |
+---+---+---+
| w | 1 | w | 
+---+---+---+
|   | w |   |
+---+---+---+

其中\(w\)需要在\([-1/4,0]\)之间，且为了保证颜色一致，锐化核中的\(1\)和\(w\)都需要除以\(1+4w\)。

对于RGB每一个通道都会单独算一个\(w\)，以R通道为例：

\[w_R = \max\left( -\frac{\min(R_i)}{4\max(R_i)}, \frac{1-\max(R_i)}{4\min(R_i)-4} \right)\]

然后需要对\(w\)的取值做一个限制：

\[w = \max\left( -\left(\frac{1}{4} - \frac{1}{16}\right), \min\left(w, 0\right) \right)\]

移动设备

MobileFSR的作者写的：移动设备上FSR的优化。

总结有以下几点：

  1. fp32 -> fp16
  2. 去掉EASU最后为了减少ringing artifacts对颜色的clip操作
  3. 计算旋转时：根据输入计算4次梯度，然后双线性插值 -> 插值输入，然后计算1次梯度
  4. 非边缘部分不再使用EASU，而是直接双线性插值（提升不大，瓶颈在纹理采样）
  5. 非边缘部分只先采样5次并插值，如果后面需要再继续插值，同时直接使用双线性插值模式的纹理采样器（代码是InputTexture.SampleLevel(samLinearClamp, p, 0)）

作者也提到，比如2和3的操作理论上是不正确的，但是带来的效果损失不大。